Building Shape/Orientation
Most often a building's shape is determined by the shape of lot and zoning considerations, so this discussion is more for those who have flexibility -- alternatively these the things to think about before you buy a lot.
There are a number of competing factor that determine shape: size of exterior surface area, daylighting and solar heat gain, with the later two being the most relevant for smaller buildings.
Materials/Energy
A cube is the most efficient way to contain a given amount of space, because it has the smallest surface area to floor area ratio--meaning it will take the least amount of materials and lose the least amount of heat for a given floor area. Because ceilings are around 8 feet, to get the minimum surface area, the building will generally need to be multiple stories. Much more relevant is that smaller building have a greater surface area to floor area ratio. The best way to see this is to look at some examples.
The following 5 house shapes are generalized from common floor plans: the square, the rectangle, skinny house and two variations on the "L" shape. The given dimensions are computed to give each shape the same amount of living space, while still choosing dimensions that are close to "real world". Each was designed to be either one room wide or two rooms wide, with a room is never deeper than 16 feet from a windows (see daylighting). Other than row houses, most buildings are never 3 rooms wide, and the reason is daylight (hint: row houses have problems there).
The following tables show the floor to surface area ratios for the various shapes and various sizes. The first chart uses the dimensions of the above example, the second is 10x bigger and the third is 1/2 the size.
Floor to Surface area ratios, 1000SF
| A | B | C | D | E | |
| 1 Story floor area | 1024 | 1025 | 1024 | 1024 | 1025 |
| 1 Story surface area | 2048 | 2081 | 2304 | 2304 | 2113 |
| 1 story floor/surface ratio | .5 | .49 | .44 | .44 | .48 |
| 2 story floor area |
2048 | 2050 | 2048 | 2048 | 2050 |
| 2 story surface area | 3200 | 3249 | 3794 | 3794 | 3337 |
| 2 story floor/surface area | .64 | .63 | .54 | .54 | .61 |
| 3 floor area | 3072 | 3075 | 3072 | 3072 | 3075 |
| 3 story surface area | 4224 | 4325 | 5024 | 5024 | 4425 |
| 3 story floor/surface ratio | .73 | .71 | .61 | .61 | .69 |
Floor to Surface area ratios, 10000SF
| A | B | C | D | E | |
| 1 Story floor area | 10,000 | 9984 | 10,000 | 10,000 | n/a |
| 1 Story surface area | 13,200 | 13,520 | 14,000 | 13,744 | n/a |
| 1 story floor/surface ratio | .76 | .74 | .71 | .73 | n/a |
| 2 story floor area | 20,000 | 19,968 | 20,000 | 20,000 | n/a |
| 2 story surface area | 16,800 | 17,480 | 18,500 | 17,956 | n/a |
| 2 story floor/surface area | 1.19 | 1.14 | 1.08 | 1.11 | n/a |
| 3 floor area | 30,000 | 29952 | 30,000 | 30,000 | n/a |
| 3 story surface area | 20,000 | 21000 | 22,500 | 22,700 | n/a |
| 3 story floor/surface ratio | 1.5 | 1.43 | 1.33 | 1.32 | n/a |
Floor to Surface area ratios, 500SF
| A | B | C | D | E | |
| 1 Story floor area | 506.25 | 500 | 504 | n/a | n/a |
| 1 Story surface area | 1226.25 | 1220 | 1368 | n/a | n/a |
| 1 story floor/surface ratio | .41 | .41 | .37 | n/a | n/a |
| 2 story floor area | 1012.5 | 1000 | 1008 | n/a | n/a |
| 2 story surface area | 2036.25 | 2030 | 2340 | n/a | n/a |
| 2 story floor/surface area | .5 | .49 | .43 | n/a | n/a |
| 3 floor area | 1518.75 | 1500 | 1512 | n/a | n/a |
| 3 story surface area | 2756.25 | 2750 | 3204 | n/a | n/a |
| 3 story floor/surface ratio | .55 | .55 | .47 | n/a | n/a |
Comparing floor area ratios tells you two things: (1) per square foot amount of material to build the envelope (2) per square foot conductive heat loss, so for example we see that the one story 500SF skinny house (shape C) has a ratio of .37, while the 3 story, 30,000SF box (shape A) has a ratio of 1.5; that is 4 times higher. The larger building is 60x bigger, but due to the improved ratio, will only take 15x more material, and for a given insulation level will only lose 15x more heat.
A few other observations:
- The difference between a square and a nearly square rectangle is minimal.
- As the building gets bigger the ratio gets better.
- Adding a story tend to improve the ratio quite a bit.
- For small buildings shape is not a huge factor.
- A typical 2-3 story skinny house uses about 10% more material and has a 10% greater conductive heat loss (however when you factor in windows and infiltration its not actually 10% worse overall).
Daylighting
The two guiding rules of thumb here at the light depth rule, and the light on two sides rule (see the daylighting section for details). The light depth rule says that no room should be deeper (distance from exterior) than 13-16'. This limits the thickness of the building to a maximum of 32'--it can be longer in the other dimension, but 32' is the limit for the smaller one, and since this dimension is two generous rooms, you can see why buildings are often laid out as 2 room X 2 rooms or 2 rooms X 3 rooms (plans A & B). All the plans above were drawn with this rule in mind, yet notice that the hallway area in plans A,B&E is likely to be dark because its far from windows and largely enclosed by walls: fortunately hallways generally need much less light than other rooms.
Next, applying the light on two sides rule, we find that the center rooms in plan B present a problem, and it becomes obvious that moving to a larger footprint, say 2 rooms X 4 rooms will just add more problems. Of the general solutions presented in the daylighting section, the one of concern here is the bump-out. On a strictly energy basis, because any bump-out increases the surface area of the building, the energy saved by good daylighting is likely swamped by heat transfer thru the additional surface--at least in all but the most benign climates. Of course light quality isn't an energy issue, so bumping out can make sense from a usability perspective even if it doesn't make energy sense.
On the above example, the one room wide plans C&D have the best daylight, but suffer the largest heat transfer--however, as has been shown, the heat transfer difference may not be that large, and hence the more elongated building might be best. But we must also consider solar gain--both wanted and unwanted.
Solar Gain
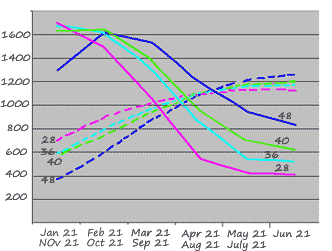
Because at temperate latitudes the sun's position in the sky is always toward the equator, the side of the building that faces that way will get more sun in the winter than in the summer, and an overhang over the window will make it easy to control the summer sun. The east and west faces, however get much more sunshine on them in summer than in winter, so a building which has a longer north-south face will have a more difficult time limiting excess summer solar gain, especially once the building is more than one story tall. This situation is can be seen from the chart at right, where April thru August the solar energy on the east and west is larger than that on the south. While the difference is less at 48° north, it is still significant: 1100Btu/day/SF on the south and a combined 2200Btu/day/SF for east and west.
For acquiring solar gain (heating climates), a rectangular building with the long axis running east/west will allow gathering the most solar energy while providing an easy way (via overhangs) to reject the summer sun. Exactly how much longer the east/west direction should be is dependent on insulation values, and climate. Ideally that east/west face should point directly south, but as long as its with about 15° of it you will still get most of the benefits.
For rejecting solar gain, the same rectangular building form applies because it is easier to shade the south side than it is the east and west. In hot climates, a north-south orientation can be better if the west sun is blocked by a hillside or other permanent barrier (for example, the west side partially dug into a hill), although doing so will still require very large overhangs on the east face (e at least eight feet), or a few small amount on glass on that side.
Other things: As the building shape emerges, keep in mind the connection to the street, maintaining the intimacy gradient, and how the landscape spaces will integrate with the indoor spaces near them.
Notes
1: Data from Appendix I, Passive Solar Energy Book, Edward Mazria, 1979.
